|
We work on several problems of high
performance networks, including switching, routing, and load
balancing. One typical aspect of the research is to establish
theoretical bounds on performance. For instance, we have a
fundamental result regarding the speedup (the speed of the
chip relative to line speed) of an input-queued switch, an
architecture consisting of buffers at the input ports. For this
architecture, a naturally predominant class of algorithms
schedule packets by first prioritizing them while they sit in the buffers.
These algorithm always fell short, until finally our work highlighted their
intrinsic limitation:
By modeling the schedule as
successive computations of weighted matchings in a bi-partite graph, it was possible
to prove that these algorithms require a speedup of at least 1.5,
regardless of the priority scheme. This result was obtained by
showing that a large bi-partite graph (e.g. representing a large
switch) must contain a weighted cycle with a special property that
limits the weight of the matching and, thus, the throughput of the
schedule.
One approach to overcome the speedup is to balance
packets across multiple switches each running at a lower speed.
Here, simple load balancing algorithms can achieve throughput probabilistically,by providing a bound on the expected length of buffers, at the cost of reordering packets.
Our current work explores the limitation of such an approach highlighting
the relationship among three
properties of load balancing: Throughput, Liveliness (will some flow starve?), and Ordering. Only
two of these can be achieved simultaneously (work in progress).
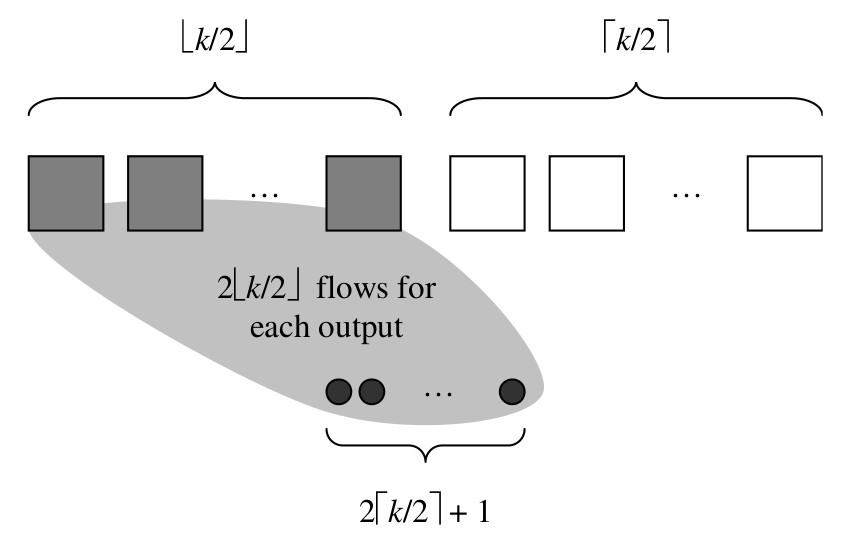
Packet reordering problem is strongly undesired in
practice. It can be avoided by routing packets of
the same flow through exactly one switch. However, using combinatorial
techniques, we proved that this family of (online) flow based algorithms
will only
achieve a throughput of at most 1/3 the maximum
throughput.
Moreover, we proved that this bound is tight by designing
an optimal online with a competitive ratio of 1/3.
Such theoretical bounds on performance are very important. For
instance, a flow based routing algorithm that achieves a 1/3
throughput is indeed optimal (since this represents the theoretical
bound). On the other hand,
knowing that every priority based algorithm must operate at a speedup of at
least 1.5, entices us to look for alternative architecture. We contributed a method to run copies of the same existing priority based
algorithm on multiple switches while avoiding any speedup per switch.
In addition,
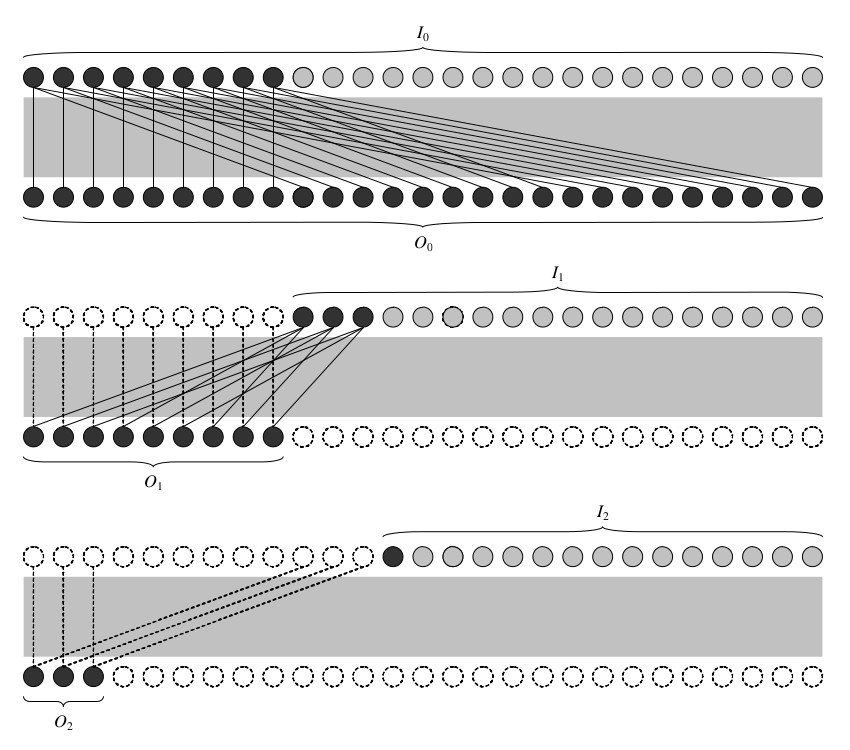
we show that it is possible to design algorithms for multiple
switches that guarantee a bounded amount of packet reordering, while
keeping full throughput, and requiring neither speedup nor the use of traditional input (or even output)
buffers.
We also work on other resource allocation problems such as balancing colored balls in bins, the carpool problem, and game theoretic
approaches for channel allocation in radio networks. Finally, we are investigating a new direction to study social networks, and other similar structures such as wikiedia pages and open source code, using simplicial complexes, a generalization of graphs where relations are not necessarily pairwise (but still form a subclass of hypergraphs).
|
|
