Our original formulation of the problem was for two RNAs, which led to the introduction of RNA-RNA interaction graphs. In these graphs, the optimal structure is given by a set of non-intersecting edges of maximum weight, which is NP-hard. We have a 2/3 factor approximation algorithm for this problem. Our notion of an "entangler" (recursive entanglers shown on the side) in the RNA-RNA interaction graph is instrumental in characterizing the sub-optimality of the predicted RNA complexes. We proved that every entangler-free solution for the RNA interaction problem is at most a 2/3 factor approximation of the optimal solution. The significance of this result lies in the fact that the wide-spread dynamic programming algorithms for the problem cannot produce entanglers, and thus are at most 2/3 optimal.

We recently pioneered a formulation for the multiple (two or more) RNA interaction problem. Multiple RNA interaction poses new computational problems which also fall under the realm of combinatorial optimization and NP-hardness. We developed approximation algorithms and, more generally, algorithms that belong to a class known as PTAS (Polynomial Time Approximation Scheme) in computer science.

In a recent development, we illustrated how the formulation can lend itself to find sub-optimal solutions efficiently. This is highly significant because it helps identify relevant biological structures that are not necessarily optimal in the computational sense. We explored randomized algorithms in conjunction with Gibbs sampling and MCMC (Monte Carlo Markov Chain). 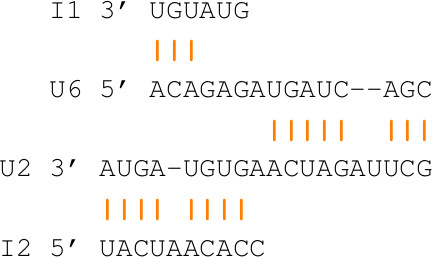To appreciate the challenges of this approach, observe that many artifact interactions can easily arise when the RNAs are exact complement of each other (they bind perfectly). The CopA-CopT complex represents such an example. It is known as the perfect couple, and has been problematic since the inception of pairwise interaction algorithms in 2005. The correct solution must drop many of these artifacts and, therefore, is typically very far from optimal and will be missed by sampling. We developed a new scoring scheme where sub-optimal solutions are not too detrimental, and hence can still show up as candidates for the sampling algorithms.

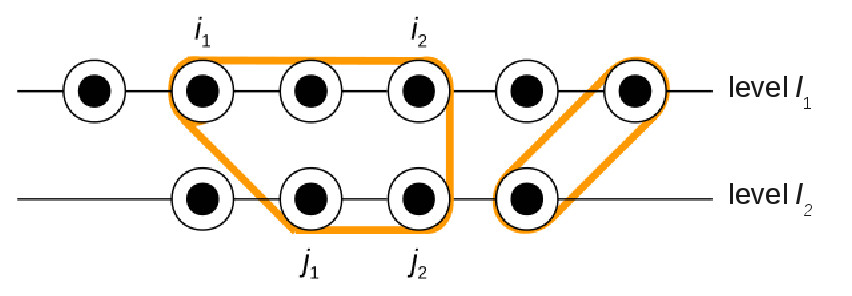
We continue to work on the multiple RNA interaction problem. The current formulation allows RNAs to interact on a path; for instance, RNA 1 interacts with RNA 2, RNA 2 interacts with RNA 3, and RNA 3 interacts with RNA 4 (as shown on the side). More recently, we extended this formulation to cycles, where in the above example RNA 4 can also interact with RNA 1. While a path or a cycle is sufficient for most RNA interactions, the order of the RNAs on the path can dramatically alter the solution. In addition, this limits each RNA to interact with at most two others. The goal is to generalize the formulation to allow paths, cycles, trees, and other types of graphs. The general problem has relations to other problems in computer science such as increasing sequences, block designs, graph arboricity, and graph decompositions.