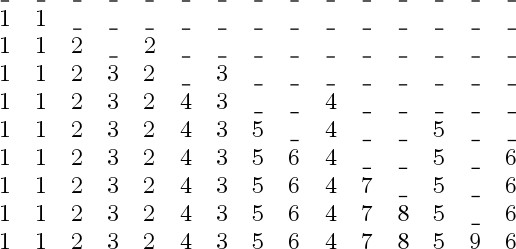
Assume each integer must occur k times for k>=2 such that the last two occurrences of every n must be at a distance of exactly n. Then the position of the first n in the sequence is given by 1 + (k - 1)(n - 1) + f(1) + f(2) + ... + f(n - 1), where f(i) is the ith bit of the infinite "Fibonacci" word given by the following grammar: start with 10, then scan the bits in order and for every 1 append the sequence with 1^{k}0, and for every 0 append the sequence with 1^{k-1}0 indefinitely, where 1^{k} means k consecutive 1s. When k=2, we get the infinite Skolem sequence shown on the side and the standard Fibonacci word. Here's an unpublished elementary proof for the case of k=2.

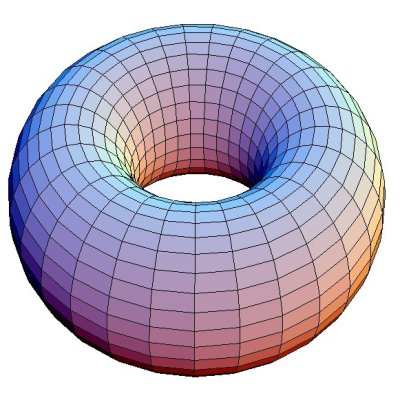
The random torus and the Golden Ratio: Imagine living on a random m x n torus where p is the probability of land and q=1-p is the probability of water. Imagine also (for good reasons) that we can walk on land following North, South, East, and West, and in water following N, S, E, W, NE, SE, NW, and SW. What value of p would make the number of islands and the number of pools roughly equal? As it turns out, this question is related to the Golden Ratio. The value of p that we seek is exactly the one that satisfies p/q=φ (p is the inverse of the golden ratio). Here's a visualization.

If we consider the expected number of islands and the expected number of pools, then at the limit when m and n go to infinity we have (an unpublished manuscript):

lim_{m, n -> ∞}{E[#islands]-E[#pools]}/(mn) = pq(q - p²).

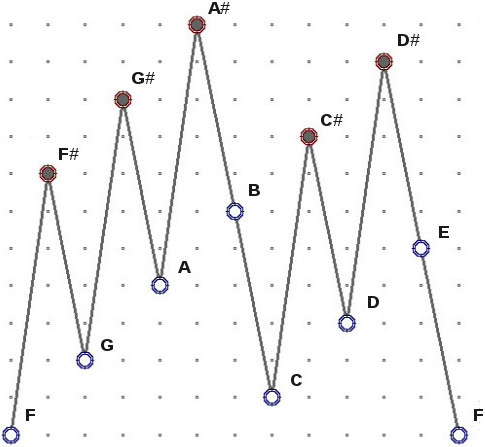
Musical scales in 2D: Consider a chromatic scale of size n. We can construct a 2D representation of such a scale by first choosing two integers a and b such that gcd(n,a)=gcd(n,b)=1. Then place in the 2D lattice the points defined by (ka,kb) for k=0, ..., n. These points define exactly two slopes, one positive and one negative, as shown on the side for n=12, a=7, and b=1. The two slopes are s=ba^{-1} mod n and s - n, where a^{-1} is the inverse of a modulo n.

It can also be shown that the lowest peak (in black) is above the highest non-peak (in white). There will be exactly min(s, n - s) peaks. These peaks represent the sharp notes, and the rest of the points define the "diatonic" scale. The idea behind this construction is to reveal a hidden component in music perception other then frequency in which sharps are really "sharp". In addition, this construction produces a diatonic scale that satisfies Myhill's property, and thus admits a generalized "circle of fifth" structure and guarantees "cardinality equals variety" and "structure implies multiplicity".

This is an ongoing research direction, but you can explore with 2D musical scales here. Choosing a and b that are not necessarily coprime with n produces interesting and funny structures.

The working secretary problem: Imagine yourself in NYC during restaurant week (well, it's actually two week long now), and that you have 14 tickets, each can be used on a separate day at any of the participating restaurants. Assume that your experience at a restaurant gives you a "score" uniformly distributed in [0,1]. Think of this as a rating of your satisfaction, which once obtained for a given restaurant, it remains unchanged. To maximize your total score for restaurant week, should you explore a different restaurant each day, or at some point stick to the one you liked the most?

This setting suggests a variant of the secretary problem where we proceed in rounds, and in each round a candidate is put on a trial period (instead of just being interviewed), and a score uniformly distributed in [0,1] is obtained. At any point in time, the interviewer can bring back the candidate with the maximum score so far (for an additional score equal to that maximum) or continues exploring new candidates in new rounds. How to maximize the total expected score if n candidates (and rounds) are available? It turns out that the best strategy is one that does not alternate, i.e. once the candidate with the maximum score is brought back, that candidate is kept for the remaining rounds.

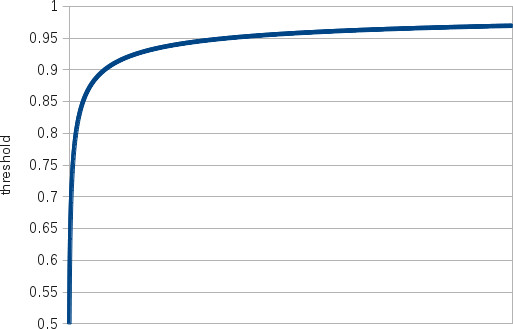
The optimal strategy compares the max so far to a threshold t_r when r rounds are left. If max>t_r, then max is used for the remaining r rounds; otherwise, a new exploration is made. The thresholds can be computed as: t_n=1, and t_r=r/[r + sqrt{r}] for 1<=r<n. The total expected score is then bounded from below by n - sqrt{n} + 0.5 and bounded from above by n - sqrt{n - 1} + 0.5.

Counting With Code: Here's my webpage for Counting With Code, a research effort aiming at a paradigm shift in the way we teach combinatorics.