By representing an amino acid sequence (protein) as a string over the alphabet {0,1,b} (hydrophillic, hydrophobic, and breaker) with probabilities p, q, and π=1-p-q respectively, we generalize the theory of percolation in one dimension and derive precise probabilities for cluster formations, where a cluster of size s consists of s "neighboring" 1s, and a b "breaks" clusters (see figure on the side). The maximum distance between neighbors (number of 0s separating them) in a cluster define the "level" k of the cluster (in standard percolation on a line, that number is always 0). For each 1, the best cluster, at some level k, is defined as the most likely among all levels. Here's a program (it's temporarily unavailable) that produces clusters given the binary version of the protein. Based on this information, we are able to map clusters to actual secondary structures in proteins, such as helices, sheets, and loops.

Micro evolution: Here the focus is on the specific type of cluster, so we make a distinction based on the level k. Using current values of p, q, and π, a random word is generated to the left and to the right of a given 1, until a breaker occurs on each side. The best cluster for that given 1, when at level k, is called a level k chunk. An infinite word for level k is constructed by repeated generation of level k chunks. Let p_k (π_k) be the probability of 1s (breakers) in such an infinite word; both of them are functions of p and π. 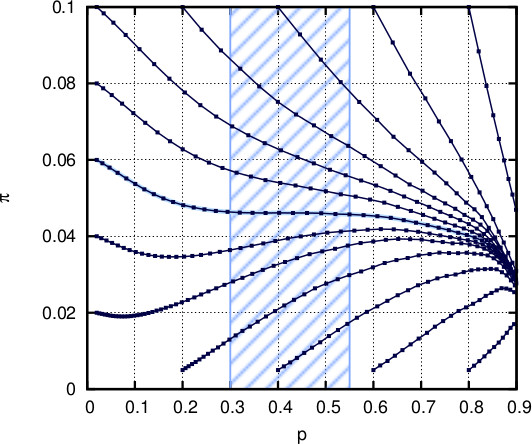Repeatedly setting p and π to the expectation of p_k and π_k over k produces a van der Waals-like plot where p and π converge to (1,0). However, in the presence of a control mechanism against unlimited growth of p, it becomes clear that π experiences a stabilization between 0.045 and 0.05 (where the curve becomes horizontal). Surprisingly, it is known that the probability of Proline is approximately 0.047. Observe that there is no external input for this evolutionary game. Furthermore, the stabilization occurs for p in [0.3, 0.55] which is consistent with the probability of hydrophobic amino acids in different species.

Macro evolution: In this evolutionary game, q is fixed at some value q_0. Given an initial b, and using current values of p, q, and π, a random word is generated until a second b occurs. The concatenation of all parts in the word that are covered by best clusters make one chunk. A infinite word is constructed by repeated generation of chunks. Let p_g (π_g) be the probability of 1s (breakers) in such an infinite word; both of them are functions of p and π. 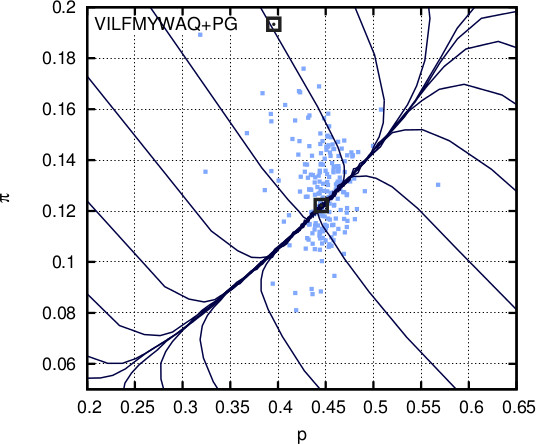Repeatedly setting p and π to p_g and π_g and conditioning on q=q_0, leads to convergence of p and π such that p+π=1-q_0. When q_0=0.43, this convergence is at (0.45,0.12), which are the probabilities of the set {V,I,L,F,Y,M,W,A,Q} and the set {P,G}, respectively. Therefore, with just q_0=0.43 as input, Glycine is revealed as another potential breaker.

The two evolutionary games reveal the existence of at least two types of breakers: An absolute breaker at the micro level, e.g. Proline, and an additional soft breaker at the macro level, e.g. Glycine. This view is consistent with Ramachandran's classification: With a rigid loop side chain, Proline lacks the flexibility to conform its phi and psi angles to almost all structures. Glycine, on the other hand, has the most flexible side chain and, therefore, is more likely than others to mediate a change of structure (thus the terminology soft breaker, acting as a mediator between clusters of different types).

This is the first and only framework that explains probability distribution of amino acids from a puristic perspective (with no reference to biological systems). We plan to extend this work to capture other biologically significant properties of proteins.